Game theory is the science of strategy. It determines how logical “players” should behave in strategic contexts and predicts the utility the “players” will reap from their actions. A “game” is any strategic set of interactions. In baseball, an example would be an at bat.

This blog leverages game theory to analyze five common scenarios in baseball. The “games” were analyzed in Python, and the graphics were developed in GIMP (the open-source version of Photoshop).

One important concept to understand before reading the remainder of this blog is Nash Equilibrium. A Nash Equilibrium occurs when the players in a game have no desire to change their decisions. Essentially, it tells us what we believe rational actors will do in a game.

The first four games are simultaneous-move games, where players make decisions at the same time. The final game is a sequential-move game, where players respond in sequence.

To note, the payoffs in the matrices below are somewhat arbitrary. They will be explained in the context of each game and should be read as relative values. In each matrix, the first payoff listed is for the row player, and the second payoff represents the column player. This structure will be more clear after we inspect the first game.

Game 1: 3-0 Pitch

This game pits hitters against pitchers. In a 3-0 pitch situation, pitchers have have two main choices: throw a pitch down the middle since the batter might be taking the pitch, or attempt to throw a quality strike on one of the corners. Likewise, a hitter has two fundamental choices: take the pitch or swing.

The matrix below displays the game and the associated payoffs. If the hitter decides to swing at a pitch down the middle, he will receive a payoff of 5 (i.e. a likely hit). The pitcher will obtain a payoff of -5, as the hitter’s gain will be the pitcher’s loss.  If the hitter swings at a pitch on the corner, we will assume he typically does not get a hit and boosts the pitcher’s confidence due to a likely swing-and-miss (payoff of -1, 1). In the case of a hitter not swinging on a pitch down the middle, he will receive a payoff of -2, as he didn’t offer at a hit-able pitch. Likewise, the pitcher will receive a payoff of 2 as he racked up an easy strike. If the hitter doesn’t swing at a pitch around the corner of the plate, he will sometimes draw a walk and other times get into a 3-1 count, netting out a payout of 0. We’ll give the pitcher a payoff of 1, as he will oftentimes throw a strike, and occasionally issuing a walk isn’t the most devastating outcome (in most cases).

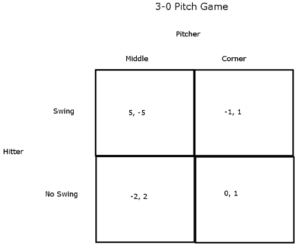
The Nash Equilibrium (NE) produces a mixed strategy. That is, hitters and pitchers should randomize their actions using a set distribution. The NE states that hitters should swing 14% of the time and take 86% of the time (hitters typically swing about 6.5% of the time in 3-0 counts). Likewise, the NE states a pitcher should throw down the middle 13% of the time and on the corner the remaining 87% of occurrences.

Game 2: 3-2 Pitch

Our next game is once again a match-up between hitters and pitchers. When the count is 3-2, pitchers face two broad choices: throw a reliable fastball to avoid a walk or be a little more risky and throw an off-speed pitch. Correspondingly, a hitter has two general decisions: anticipate a fastball or anticipate an off-speed pitch.

When a hitter correctly anticipates a fastball, he will get a large payoff. Likewise, when he correctly guesses an off-speed pitch, he gets a nice payoff, though not quite as large as when he correctly anticipates the fastball. Pitchers obtain high payoffs when inducing the hitter to make an incorrect guess.

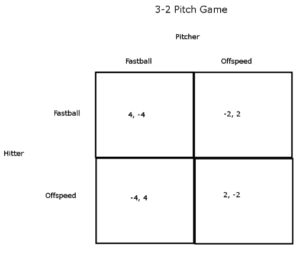
The 3-2 pitch game also produces a mixed-strategy NE. Hitters should anticipate a fastball 50% of the time and anticipate an off-speed pitch 50% of the time. Pitchers should hurl a fastball in 33% of cases and throw an off-speed pitch in 67% of cases. From the payoff matrix, we see that a pitcher is safer throwing off-speed pitches. Their max payoff is 2, and their min payoff is -2. The fastball is riskier, with a potential min payoff of -4, though the max payoff is 4. For the hitter, guessing fastball leads to either a big payoff or a moderate loss. Anticipating an off-speed pitch produces either a large loss or a modest payoff.

Game 3: Free Agent Competition

Teams competing for a free agent is also a classic example of game theory. In this example, we will limit the competition to two teams working to sign one players. We will constrain each team’s choices to two options: make a high offer or make a low offer.

I won’t explain the payoffs of this game…I’ll let the reader give it a shot.

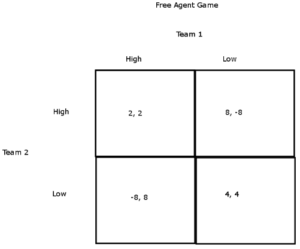
This game is different from the previous two: the NE is a single strategy. Both teams should make high offers. The maximum joint payoff is where both teams make low offers. However, if one team makes a low offer, the other team has a huge incentive to make a high offer. In such an instance, the second team would sign the player and “win” the game. This game partly explains why some players receive massive contracts. Teams would be better off if they colluded and made low offers to players; eventually, the players would accept if they wanted to continue competing. However, teams would always have the incentive to cheat on the collusion agreement.

Game 4: Switching Pitchers

Our next example of game theory in baseball involves switching pitchers and/or hitters to get a more favorable match-up late in a game. Typically, this scenario would constitute a sequential-move game; however, we will model it as a simultaneous-move game here. Imagine that managers are behind a curtain and must make their decision without knowing what the other manager has decided.

When both teams switch, we will assume those moves essentially cancel each other out. We will also assume that when one team switches and the other doesn’t, the team making the switch obtains a higher payoff. Further, we will give the offense a slight advantage in the case where neither team makes a switch.

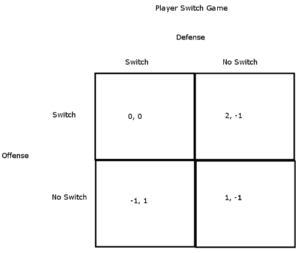
Like the last one, this game suggests each team should always play a single strategy: switch.

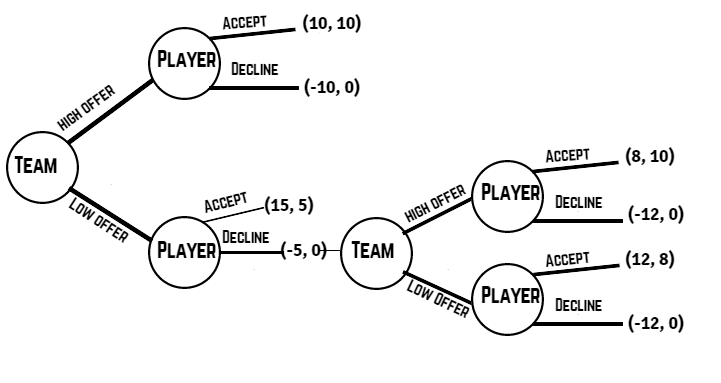
Game 5: Contract Negotiation

The game below is different from the previous ones; it is a sequential-move game. The game lays out a sequence of possible decisions in a contract negotiation between a team and a player. Take a look at the game below and see if you can deduce the outcome. (We will discuss it, too).

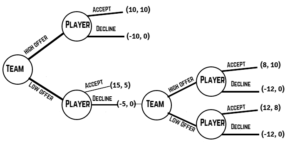
In this game, a team can either make a high offer or a low offer, and a player can either accept or reject the offer. We can solve such a game by looking ahead and reasoning back. If we employ such a strategy, we see the game will end with a player accepting a low offer (in this game, payoffs are listed with the team first and the player second). The team will receive a payoff of 12, and the player will receive a payoff of 8.

To note, we will assume the second low offer is higher than the first low offer, but still lower than a high offer.

If the team makes a low offer, they know the player will decline the offer. How? The player knows that by declining the offer, they will obtain a better payoff. How? They can forecast the team will make another low offer (though higher than the initial low offer). How do they know this? Because they see that the team will receive its highest possible payoff by making the second low offer (12). The player will accept this offer as a payoff of 8 is better than 0. The team would never counter with a high offer because they know the player would accept, and the team would only get a payoff of 8. Likewise, the player would never accept the first low offer and take a payoff of 5, as they can look ahead and see they would later get a payoff of 8. Further, a team would never start with a high offer. By looking ahead, they know an initial high offer results in a payoff of 10, whereas an initial low offer eventually produces a payoff of 12.

Conclusion

Game theory is pretty nifty, right? Baseball is full of strategic interactions, and game theory can assist us in analyzing them in a structured way.